Introduction :
I. KNN : Comment ça marche ?






Source : https://www.science.lu/fr/bande-dessinee/frontiere-entre-sciences-biomedicales-informatiques
2. L’algorithme des k plus proches voisins : principe général
Le principe
3. L’algorithme des k plus proches voisins : exemple pratique
Historique
En 1936, Edgar Anderson a collecté des données sur 3 espèces d’iris : « iris setosa », « iris virginica » et « iris versicolor ».
Pour chaque iris étudié, Anderson a mesuré (en cm) :
Par souci de simplification, nous nous intéresserons uniquement à la largeur et à la longueur des pétales. Pour chaque iris mesuré, Anderson a aussi noté l’espèce (« iris setosa », « iris virginica » ou « iris versicolor »)
Vous trouverez 50 de ces mesures dans un fichier iris.csv
En résumé, vous trouverez dans ce fichier :
- la longueur des pétales
- la largeur des pétales
- l’espèce de l’iris (au lieu d’utiliser les noms des espèces, on utilisera des chiffres : 0 pour « iris setosa », 1 pour « iris virginica » et 2 pour « iris versicolor »)
Données CSV à télécharger (pour voir à quoi ressemblent les données) :
Activité :
Partie A :
Question 1 : Ajoutez des commentaires pour légender l’utilité de chaque groupe de lignes.
Programme :
import pandas
import matplotlib.pyplot as plt
iris=pandas.read_csv(« https://pixees.fr/informatiquelycee/n_site/asset/iris.csv »)
x=iris.loc[:, »petal_length »]
y=iris.loc[:, »petal_width »]
lab=iris.loc[:, »species »]
plt.scatter(x[lab == 0], y[lab == 0], color=’g’, label=’setosa’)
plt.scatter(x[lab == 1], y[lab == 1], color=’r’, label=’virginica’)
plt.scatter(x[lab == 2], y[lab == 2], color=’b’, label=’versicolor’)
plt.legend()
plt.show()
Sortie :
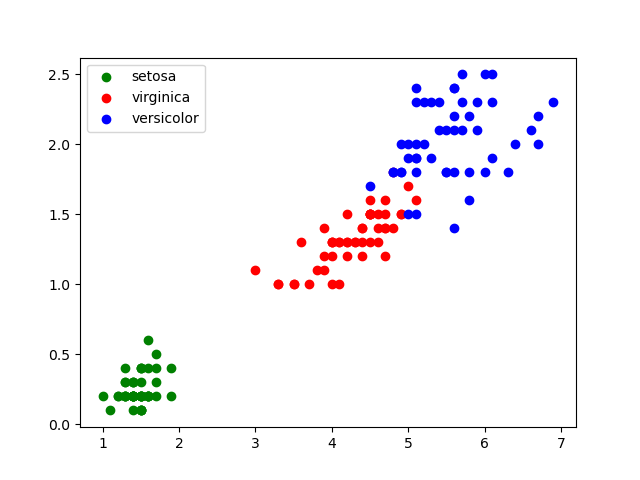
Partie B :
On exécute le programme suivant pour classifier une fleur inconnue en faisant varier la longueur et la largeur.
Programme :
import pandas
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
#traitement CSV
iris=pandas.read_csv(« http://pixees.fr/informatiquelycee/n_site/asset/iris.csv »)
x=iris.loc[:, »petal_length »]
y=iris.loc[:, »petal_width »]
lab=iris.loc[:, »species »]
#fin traitement CSV
#valeurs
longueur=4.9
largeur=1.6
k=3
#fin valeurs
#graphique
plt.scatter(x[lab == 0], y[lab == 0], color=’g’, label=’setosa’)
plt.scatter(x[lab == 1], y[lab == 1], color=’r’, label=’virginica’)
plt.scatter(x[lab == 2], y[lab == 2], color=’b’, label=’versicolor’)
plt.scatter(longueur, largeur, color=’y’, label=’à catégoriser’)
plt.legend()
#fin graphique
#algo knn
d=list(zip(x,y))
model = KNeighborsClassifier(n_neighbors=k)
model.fit(d,lab)
prediction= model.predict([[longueur,largeur]])
#fin algo knn
#Affichage résultats
txt= »Résultat : «
if prediction[0]==0:
txt=txt+ »setosa »
if prediction[0]==1:
txt=txt+ »virginica »
if prediction[0]==2:
txt=txt+ »versicolor »
#fin affichage résultats
plt.text(3,0.5, « largeur : {} cm longueur : {} cm ».format(largeur,longueur), fontsize=12)
plt.text(3,0.3, « k : {} ».format(k), fontsize=12)
plt.text(3,0.1, txt, fontsize=12)
plt.show()
Sortie pour différentes valeurs de longueur et largeur, mais k constant. Cliquez sur les images pour les agrandir.
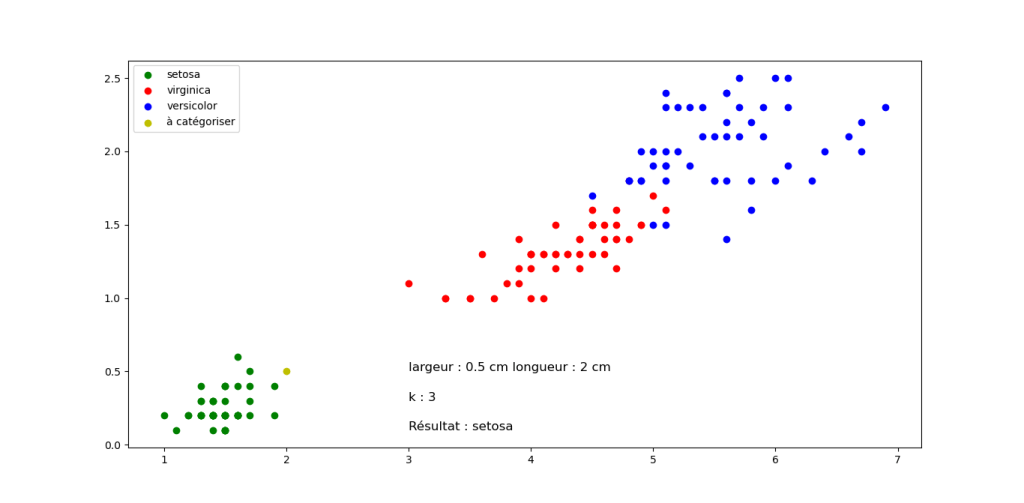
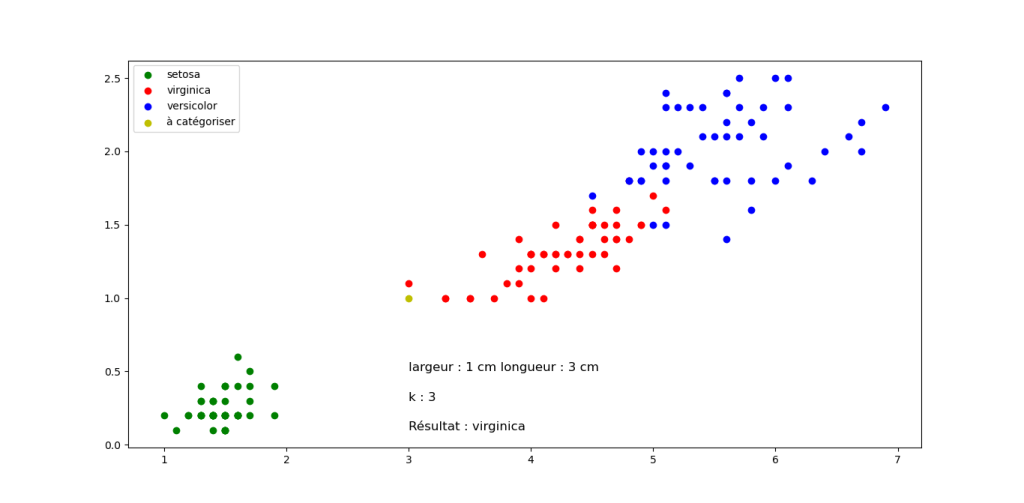
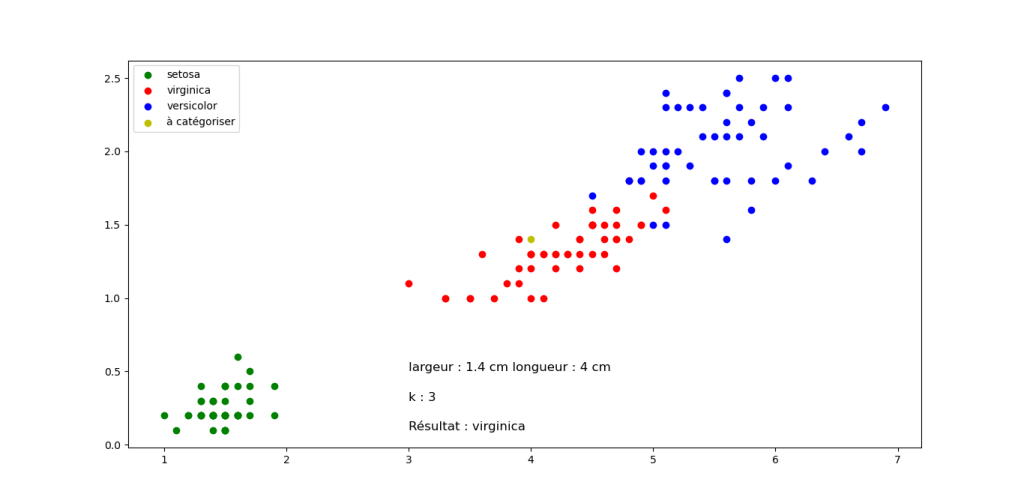
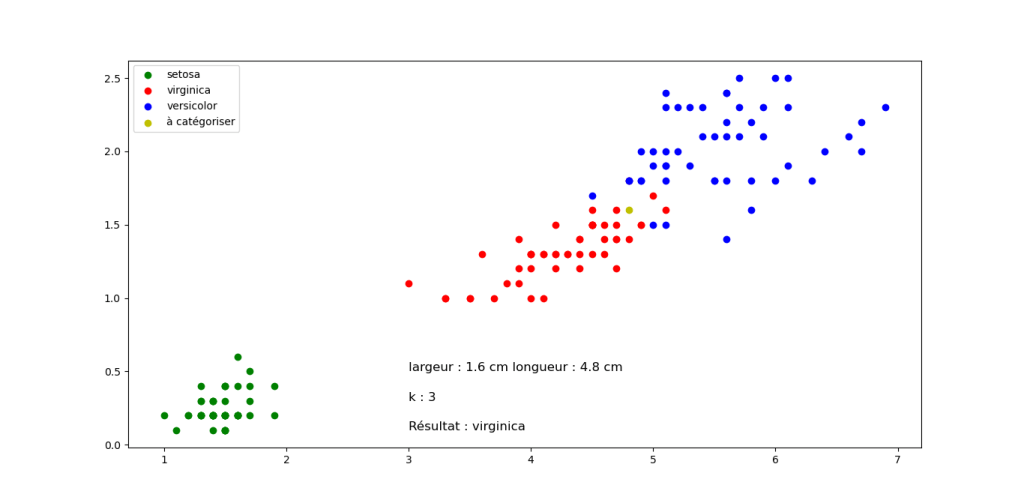
Question 2 : Quelle classification proposez vous pour les fleurs suivantes en sachant que k=3 pour tous les exemples (Justifier votre réponse). Cliquez sur les images pour les agrandir.
Fleur A
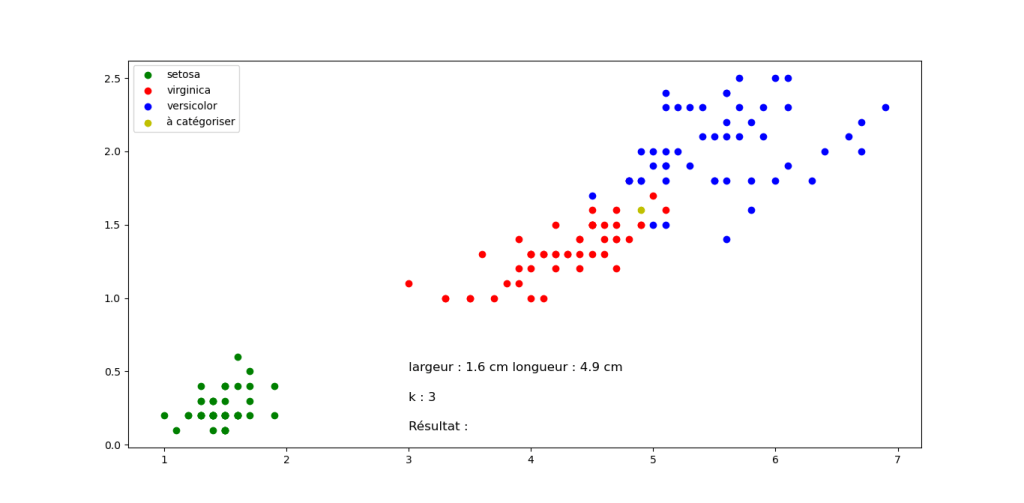
Fleur B
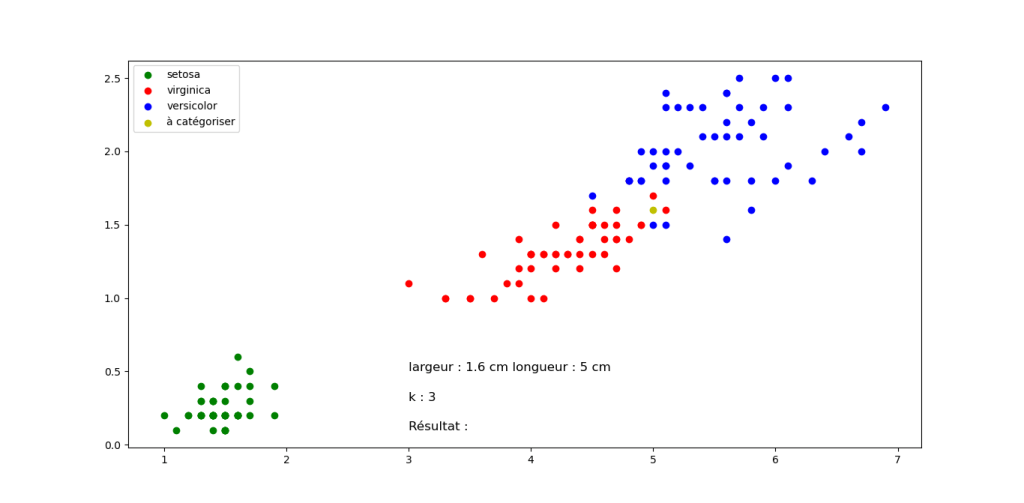
Fleur C
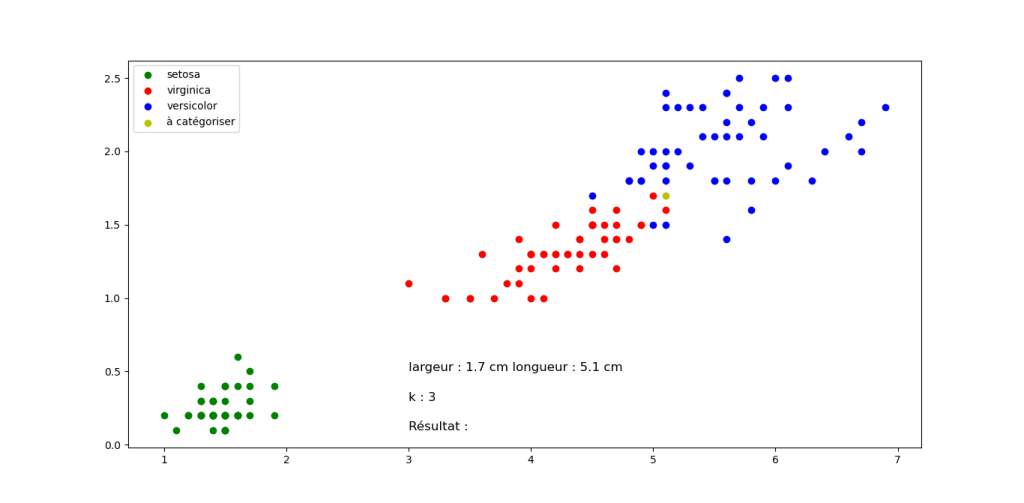
Fleur D
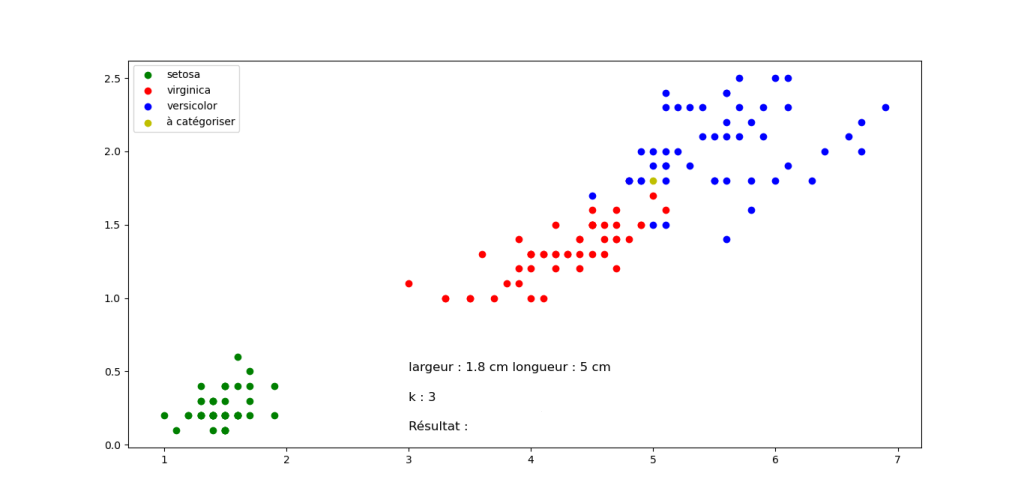
Fleur E
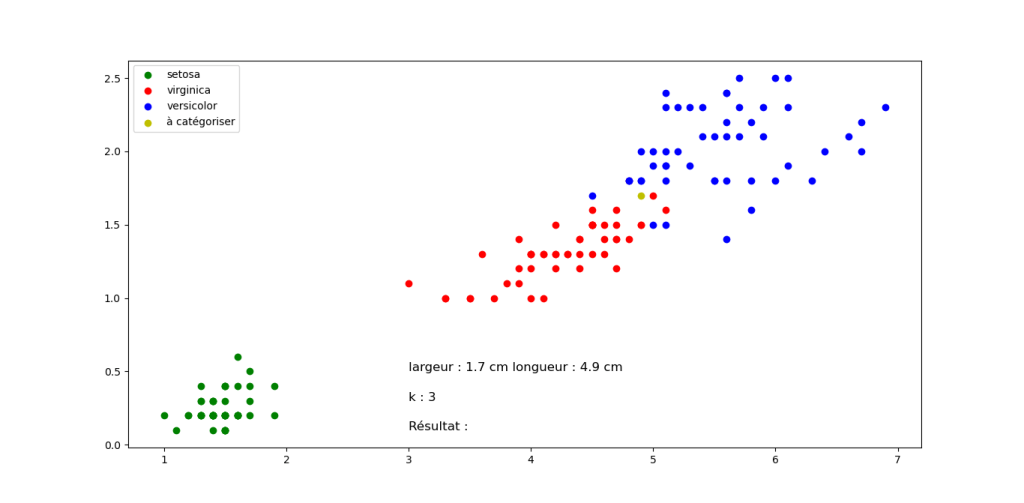
Fleur F
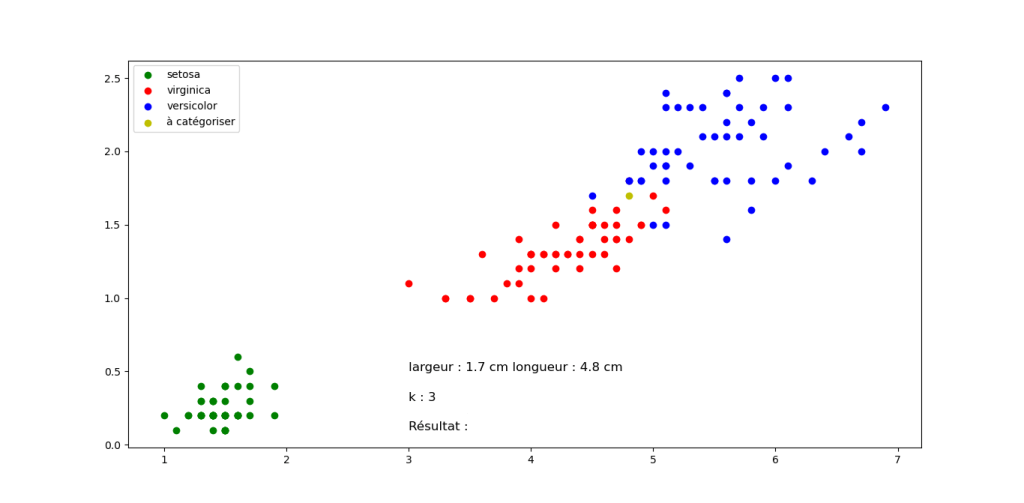
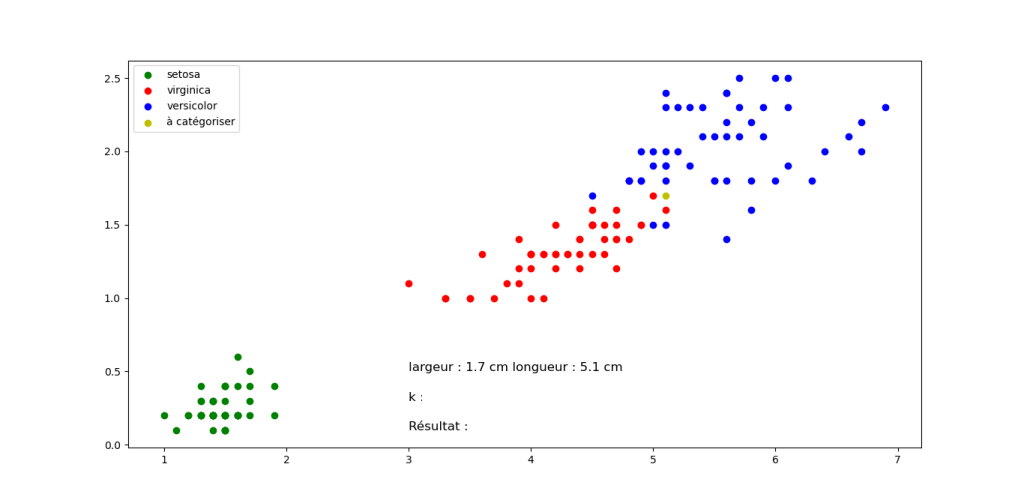
Question 3 : On fait varier la valeur de k pour une position de longueur et de largeur fixe. Proposez vos résultats de classification pour des valeurs de k =3, 5 et 7

Ecrit par Picassciences
Poster un commentaire